С-Петербург, улица Тосина 3
+7 (812) 917-84-85
+7 (921) 316-27-00
Главная » Разное » Механика для чайников

Механика для чайников


Основы механики для чайников. Введение

В рамках любого учебного курса изучение физики начинается с механики. Не с теоретической, не с прикладной и не вычислительной, а со старой доброй классической механики. Эту механику еще называют механикой Ньютона. По легенде, ученый гулял по саду, увидел, как падает яблоко, и именно это явление подтолкнуло его к открытию закона всемирного тяготения. Конечно, закон существовал всегда, а Ньютон лишь придал ему понятную для людей форму, но его заслуга – бесценна. В данной статье мы не будем расписывать законы Ньютоновской механики максимально подробно, но изложим основы, базовые знания, определения и формулы, которые всегда могут сыграть Вам на руку.

Механика – раздел физики, наука, изучающая движение материальных тел и взаимодействия между ними.

Само слово имеет греческое происхождение и переводится как «искусство построения машин» . Но до построения машин нам еще как до Луны, поэтому пойдем по стопам наших предков, и будем изучать движение камней, брошенных под углом к горизонту, и яблок, падающих на головы с высоты h.

Исаак Ньютон

Почему изучение физики начинается именно с механики? Потому что это совершенно естественно, не с  термодинамического же равновесия его начинать?!

Механика – одна из старейших наук, и исторически изучение физики  началось именно с основ механики. Помещенные в рамки времени и пространства, люди, по сути, никак не могли начать с чего-то другого, при всем желании. Движущиеся тела – первое, на что мы обращаем  свое внимание.

 Что такое движение?

Механическое движение – это изменение положения тел в пространстве относительно друг друга с течением времени.

Именно после этого определения мы совершенно естественно приходим к понятию системы отсчета. Изменение положения тел в пространстве относительно друг друга.  Ключевые слова здесь: относительно друг друга. Ведь пассажир в машине движется относительно стоящего на обочине человека с определенной скоростью, и покоится относительно своего соседа на сиденье рядом, и движется с какой-то другой скоростью относительно пассажира в машине, которая их обгоняет.

Механическое движение

Именно поэтому, для того, чтобы нормально измерять параметры движущихся объектов и не запутаться, нам нужна система отсчета - жестко связанные между собой тело отсчета,  система координат и часов. Например, земля движется вокруг солнца в гелиоцентрической системе отсчета. В быту практически все свои измерения мы проводим в геоцентрической системе отсчета, связанной с Землей. Земля – тело отсчета, относительно которого движутся машины, самолеты, люди, животные.

Система отсчета, связанная с землей - геоцентрическая

Механика, как наука, имеет свою задачу. Задача механики – в любой момент времени знать положение тела в пространстве. Иными словами, механика строит математическое описание движения и находит связи между физическими величинами, его характеризующими.

Для того, чтобы двигаться далее, нам понадобится понятие “материальная точка”. Говорят, физика – точная наука, но физикам известно, сколько приближений и допущений приходится делать, чтобы согласовать эту самую точность. Никто никогда не видел материальной точки и не нюхал идеального газа, но они есть! С ними просто гораздо легче жить.

Материальная точка – тело, размерами и формой которого в контексте данной задачи можно пренебречь.

Разделы классической механики

Механика состоит из нескольких разделов

  • Кинематика
  • Динамика
  • Статика

Кинематика с физической точки зрения изучает, как именно тело движется. Другими словами, этот раздел занимается количественными характеристиками движения. Найти скорость, путь – типичные задачи кинематики

Динамика решает вопрос, почему оно движется именно так. То есть, рассматривает силы, действующие на тело.

Статика изучает равновесие тел под действием сил, то есть отвечает на вопрос: а почему оно вообще не падает?

Границы применимости классической механики.

Классическая механика уже не претендует на статус науки, объясняющей все (в начале прошлого века все было совершенно иначе), и имеет четкие рамки применимости. Вообще, законы классической механики справедливы привычном нам по размеру мире (макромир). Они перестают работать в случае мира частиц, когда на смену классической приходит квантовая механика. Также классическая механика неприменима к случаям, когда движение тел происходит со скоростью, близкой к скорости света. В таких случаях ярко выраженными становятся релятивистские эффекты. Грубо говоря, в рамках квантовой и релятивистской механики – классическая механика, это частный случай, когда размеры тела велики, а скорость – мала. Подробнее об распознавании сканированного текста вы можете узнать из нашей статьи.

Движение на скорости, близкой к скорости света, нельзя описать законами классической механики

Вообще говоря, квантовые и релятивистские эффекты никогда никуда не деваются,  они имеют место быть и при обычном движении макроскопических тел со скоростью, много меньшей скорости света. Другое дело, что действие этих эффектов так мало, что не выходит за рамки самых точных измерений. Классическая механика, таким образом, никогда не потеряет своей фундаментальной важности.

Мы продолжим изучение физических основ механики в следующих статьях. Для лучшего понимания механики Вы всегда можете обратиться к нашим авторам, которые в индивидуальном порядке прольют свет на темное пятно самой сложной задачи.

Основы механики для "чайников" (часть 3): релятивистская механика

Релятивистская механика

Релятивистская механика – это механика, в которую превращается механика Ньютона в случае если тело движется со скоростью, близкой к скорости света. На таких высоких скоростях с вещами начинают происходить ну просто волшебные и совершенно неожиданные вещи, такие как, например, релятивистское сокращение длины или замедление времени.

Но как именно классическая механика становится релятивистской? Обо всем по порядку в нашей новой статье.

Начнем с самого начала...

Принцип относительности Галилея

Принцип относительности Галилея (1564-1642) гласит:

В инерциальных системах отсчета все процессы протекают одинаково, если система неподвижна или движется равномерно и прямолинейно.

В данном случае речь идет исключительно о механических процессах. Что это значит? Это значит, что если мы, например, будем плыть на равномерно и прямолинейно движущемся пароме через туман, мы не сможем определить, движется паром или покоится. Иными словами, если провести эксперимент в двух одинаковых замкнутых лабораториях, одна из которых равномерно и прямолинейно движется относительно другой, результат эксперимента будет одинаковым.

Галилео Галилей

Преобразования Галилея

Преобразования Галилея в классической механике – это преобразования координат и скорости при переходе от одной инерциальной системы отсчета к другой. Не будем приводить здесь всех вычислений и выводов, а просто запишем формулу для преобразования скорости. Согласно этой формуле скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела в движущейся системе отсчета и скорости движущейся системы отсчета относительно неподвижной.

Приведенный нами выше принцип относительности Галилея является частным случаем принципа относительности Эйнштейна.

Принцип относительности Эйнштейна и постулаты СТО

В начале двадцатого века после более чем двухсотлетнего господства классической механики возник вопрос о распространении принципа относительности на немеханические явления. Причиной возникновения такого вопроса стало закономерное развитие физики, в частности оптики и электродинамики. Результаты многочисленных экспериментов то подтверждали справедливость формулировки принципа относительности Галилея для всех физических явлений, то в ряде случаев указывали на ошибочность преобразований Галилея.

Эйнштейн - человек, создавший специальную теорию относительности

Например, проверка формулы сложения скоростей показала ее ошибочность при скоростях, близких к скорости света. Более того, опыт Физо в 1881 году показал, что скорость света не зависит от скорости движения источника и наблюдателя, т.е. в любой системе отсчета остается постоянной. Данный результат эксперимента никак не укладывался в рамки классической механики.

Решение этой и других проблем нашел Альберт Эйнштейн. Для того чтобы теория сошлась с практикой, Эйнштейну пришлось отказаться от нескольких, казалось бы, очевидных истин классической механики. А именно - предположить, что расстояния и промежутки времени в различных системах отсчета не неизменны. Ниже приведем основные постулаты Специальной Теории Относительности (СТО) Эйнштейна:

Первый постулат: во всех инерциальных системах отсчета все физические явления протекают одинаково.  При переходе от одной системы к другой все законы природы и явления, описывающие их,  инвариантны, то есть никакими опытами нельзя отдать предпочтение одной из систем, ибо они инвариантны.

Второй постулат: скорость света в вакууме одинакова во всех направлениях и не зависит от источника и наблюдателя, т.е. не изменяется при переходе от одной инерциальной системы к другой.

Скорость света – предельная скорость. Никакой сигнал или действие не могут распространяться со скоростью, превышающей скорость света.

Преобразования координат и времени при переходе от неподвижной системы отсчета к системе, движущейся со скоростью света, называются преобразованиями Лоренца. Кпримеру, пусть одна система покоится, а вторая движется вдоль оси абсцисс.

Здесь

Как видим, время также изменяется наряду с координатами, то есть выступает как бы в роли четвертной координаты. Преобразования Лоренца показывают, что в СТО пространство и время неразделимы в отличие от классической механики.

Помните парадокс двух близнецов, один из которых ждал на земле, а второй летел на космическом корабле с очень большой скоростью? После того как брат-космонавт вернулся на землю, он застал своего брата стариком, хотя сам был практически так же молод, как в момент начала путешествия. Типичный пример того, как изменяется время в зависимости от системы отсчета.

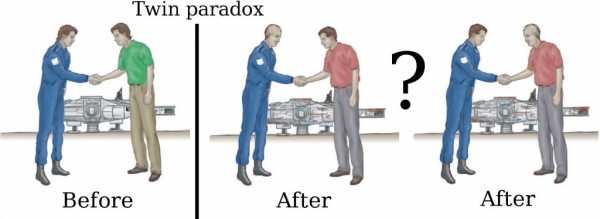Парадокс близнецов

При скоростях же много меньших скорости света преобразования Лоренца переходят в преобразования Галилея. Даже при скорости современных реактивных самолетов и ракет отклонения от законов классической механики настолько малы, что их практически невозможно измерить.

Релятивистская механика

Механика, учитывающая преобразования Лоренца,  и называется релятивистской.

В рамках релятивистской механики меняются формулировки некоторых физических величин. Например, импульс тела в релятивистской механике в соответствии с преобразованиями Лоренца может быть записан так:

Соответственно, второй закон Ньютона в релятивистской механике будет иметь вид:

А полная релятивистская энергия тела в релятивистской механике равна

Если тело покоится и скорость равна нулю, данная формула преобразуется в знаменитую

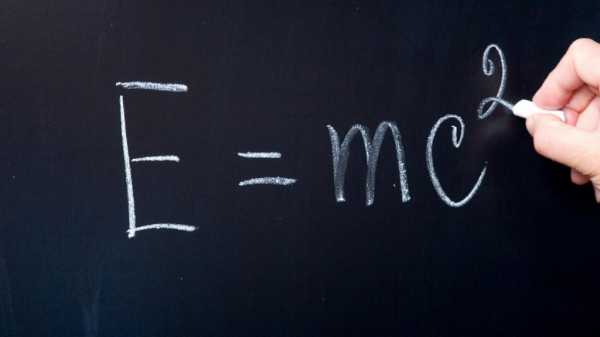Формула энергии покоя тела

Данная формула, которую, кажется, знают все, показывает, что масса является мерой полной энергии тела, а также иллюстрирует принципиальную возможность перехода энергии вещества в энергию излучения.

Дорогие друзья, на этой торжественной ноте мы закончим наш сегодняшний обзор релятивистской механики. Мы рассмотрели принцип относительности Галилея и Эйнштейна, а также некоторые основные формулы релятивистской механики. Самым стойким и дочитавшим статью до конца напоминаем – в мире нет «нерешабельных» задач и проблем, которые невозможно решить. Паниковать и переживать из-за незаконченной курсовой нет никакого смысла. Просто вспомните о масштабах Вселенной, вздохните полной грудью и поручите выполнение настоящим профессионалам своего дела – авторам компании Zaochnik.

Основы механики для "чайников". Часть 2: Динамика

Динамика изучает причины, по которым движение происходит именно так, а не иначе. Ее интересуют силы, которые действуют на тела. У динамики есть прямая и обратная задачи. Прямая - по известному характеру движения определить равнодействующую всех сил, действующих на тело. Обратная - по заданным силам определить характер движения тела. Конечно, мы должны познакомиться с понятием силы, инерциальной системы отсчета, законами Ньютона. Но обо всех основах динамики по порядку. В данной статье рассмотрим основные законы динамики и приведем пример решения задачи по основам динамики.

В чем сила, брат?

Красота – страшная сила! А еще, конечно, сила в правде, а у кого-то в деньгах. Но мы-то знаем, что все это заблуждения и домыслы. Сила – в Ньютонах!

Сила. Измеряется в Ньютонах

Сила – векторная физическая величина, количественная мера интенсивности взаимодействия тел.

Единицей измерения силы в системе СИ является Ньютон. Один Ньютон – это такая сила, которую мы можем приложить к телу массой один килограмм. При этом она изменит скорость тела на 1 м/с за одну секунду.

Бывает , что на тело действует сразу несколько сил. В принципе, в мире нет тел и предметов, на которые не действуют вообще никакие силы. Вот с утра едем мы на экзамен, и так бы нам хотелось, чтоб никакие силы нас не трогали и оставили в покое... Но нет. Притяжение давит вниз, ветер сдувает вбок, кто-то еще нагло толкает в метро. В таком случае можно все эти силы представить как одну, но оказывающую то же действие, что и все. Векторная сумма всех сил, действующих на тело, называется равнодействующей силой.

Например, на рисунке ниже равнодействующая сил равна нулю, потому как лебедь рак и щука так никуда и не сдвинули воз.

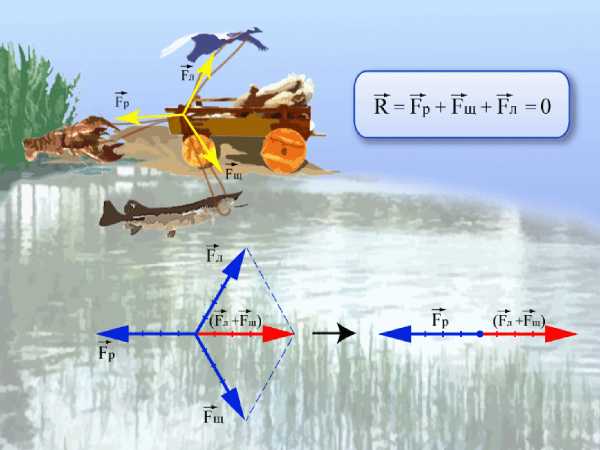Равнодействующая сила

Масса и Вес

Масса – скалярная аддитивная физическая величина, являющаяся количественной мерой инертности тела, то есть его способности сохранять постоянную скорость.

В системе СИ измеряется в килограммах.  Если не ищете легких путей и хотите быть особенно экстравагантным, можете измерять в фунтах, пудах и унциях.

Важно! Не стоит путать массу тела и вес. Ведь масса – скалярная величина, а вес – это сила, с которой тело действует на опору или подвес. Другими словами, масса всегда остается постоянной, это собственная характеристика тела. А вот вес может меняться. Например, Ваш лунный вес будет отличаться от земного, т.к. ускорение свободного падения на планетах различно.

Вы все еще читаете? Поздравляем, Вы просто молодцы! Давайте переходить к законам Ньютона, ведь рассматривая основы динамики невозможно обойти их стороной. Законы Ньютона - основные законы динамики.

Первый закон Ньютона

Как мы уже знаем, движение осуществляется в системе отсчета. Так вот, существуют такие системы отсчета, которые называются инерциальными (ИСО). Что это значит? Это тоже идеализация, наподобие материальной точки. Существование ИСО постулируется первым законом Ньютона, который собственно гласит вот что:

Существуют системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно или покоятся, если на них не действуют никакие силы, или действие других сил скомпенсировано (равнодействующая равна нулю).

Если в инерциальной системе отсчета мы разгоним автомобиль до скорости 60 км/ч, пренебрежем силой трения колес об асфальт и сопротивлением воздуха, а потом выключим двигатель, авто продолжит катиться по прямой со скоростью 60 км/ч бесконечно долго, пока не закончится дорога.

Второй закон Ньютона

Второй закон Ньютона еще называют основным законом динамики. Самая простая его формулировка такова:

В ИСО ускорение, приобретаемое телом, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе тела.

Еще одна формулировка второго закона Ньютона: производная импульса материальной точки по времени равна действующей на материальную точку силе. Импульс – мера количества движения, равняется произведению массы на скорость.

Действительно, вспомним кинематику (производная от скорости равна ускорению) и запишем:

Третий закон Ньютона

В ИСО тела действуют друг на друга с силами, лежащими на одной прямой, противоположными по направлению и равными по модулю.

Напоследок, как всегда, приведем пример решения задачи на основы динамики.

Брусок массой 5кг тянут по горизонтальной поверхности за веревку, составляющую угол 30 градусов с горизонтом. Сила натяжения веревки – 30 Ньютонов. За 10 секунд, двигаясь равноускоренно, брусок изменил скорость с 2 м/с до 12 м/с. Найти коэффициент трения бруска о плоскость.

Решение:

Нарисуем брусок. На него действуют сила тяжести, сила нормальной реакции опоры, сила трения и сила натяжения веревки. Веревку будем считать нерастяжимой. Первым делом найдем ускорение бруска, а затем вычислим проекцию сил на горизонтальную ось и запишем второй закон Ньютона.

Основы динамики в физике очень важны для понимания процесса движения. Помните, друзья, в экстремальных условиях сессии наши авторы всегда готовы поддержать Вас и облегчить учебную нагрузку. Удачи Вам!

Теоретическая механика. В помощь студенту

Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.

Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.

Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.

Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.

Статика твердого тела

Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.

    Основные понятия и законы статики
  • Абсолютно твердое тело (твердое тело, тело) – это материальное тело, расстояние между любыми точками в котором не изменяется.
  • Материальная точка – это тело, размерами которого по условиям задачи можно пренебречь.
  • Свободное тело – это тело, на перемещение которого не наложено никаких ограничений.
  • Несвободное (связанное) тело – это тело, на перемещение которого наложены ограничения.
  • Связи – это тела, препятствующие перемещению рассматриваемого объекта (тела или системы тел).
  • Реакция связи — это сила, характеризующая действие связи на твердое тело. Если считать силу, с которой твердое тело действует на связь, действием, то реакция связи является противодействием. При этом сила — действие приложена к связи, а реакция связи приложена к твердому телу.
  • Механическая система – это совокупность взаимосвязанных между собой тел или материальных точек.
  • Твердое тело можно рассматривать как механическую систему, положения и расстояние между точками которой не изменяются.
  • Сила – это векторная величина, характеризующая механическое действие одного материального тела на другое. Сила как вектор характеризуется точкой приложения, направлением действия и абсолютным значением. Единица измерения модуля силы – Ньютон.
  • Линия действия силы – это прямая, вдоль которой направлен вектор силы.
  • Сосредоточенная сила – сила, приложенная в одной точке.
  • Распределенные силы (распределенная нагрузка) – это силы, действующие на все точки объема, поверхности или длины тела. Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины).

    Размерность распределенной нагрузки – Н/м3 (Н/м2, Н/м).

  • Внешняя сила – это сила, действующая со стороны тела, не принадлежащего рассматриваемой механической системе.
  • Внутренняя сила – это сила, действующая на материальную точку механической системы со стороны другой материальной точки, принадлежащей рассматриваемой системе.
  • Система сил – это совокупность сил, действующих на механическую систему.
  • Плоская система сил – это система сил, линии действия которых лежат в одной плоскости.
  • Пространственная система сил – это система сил, линии действия которых не лежат в одной плоскости.
  • Система сходящихся сил – это система сил, линии действия которых пересекаются в одной точке.
  • Произвольная система сил – это система сил, линии действия которых не пересекаются в одной точке.
  • Эквивалентные системы сил – это такие системы сил, замена которых одна на другую не изменяет механического состояния тела. Принятое обозначение: .
  • Равновесие – это состояние, при котором тело при действии сил остается неподвижным или движется равномерно прямолинейно.
  • Уравновешенная система сил – это система сил, которая будучи приложена к свободному твердому телу не изменяет его механического состояния (не выводит из равновесия). .
  • Равнодействующая сила – это сила, действие которой на тело эквивалентно действию системы сил. .
  • Момент силы – это величина, характеризующая вращающую способность силы.
  • Пара сил – это система двух параллельных равных по модулю противоположно направленных сил. Принятое обозначение: . Под действием пары сил тело будет совершать вращательное движение.
  • Проекция силы на ось – это отрезок, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой оси. Проекция положительна, если направление отрезка совпадает с положительным направлением оси.
  • Проекция силы на плоскость – это вектор на плоскости, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой плоскости.
  • Закон 1 (закон инерции). Изолированная материальная точка находится в покое либо движется равномерно и прямолинейно. Равномерное и прямолинейное движение материальной точки является движением по инерции. Под состоянием равновесия материальной точки и твердого тела понимают не только состояние покоя, но и движение по инерции. Для твердого тела существуют различные виды движения по инерции, например равномерное вращение твердого тела вокруг неподвижной оси.
  • Закон 2. Твердое тело находится в равновесии под действием двух сил только в том случае, если эти силы равны по модулю и направлены в противоположные стороны по общей линии действия. Эти две силы называются уравновешивающимися.

    Вообще силы называются уравновешивающимися, если твердое тело, к которому приложены эти силы, находится в покое.

  • Закон 3. Не нарушая состояния (слово «состояние» здесь означает состояние движения или покоя) твердого тела, можно добавлять и отбрасывать уравновешивающиеся силы. Следствие. Не нарушая состояния твердого тела, силу можно переносить по ее линии действия в любую точку тела. Две системы сил называются эквивалентными, если одну из них можно заменить другой, не нарушая состояния твердого тела.
  • Закон 4. Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке, равна по модулю диагонали параллелограмма, построенного на этих силах, и направлена вдоль этой диагонали. По модулю равнодействующая равна:

  • Закон 5 (закон равенства действия и противодействия). Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены в противоположные стороны по одной прямой. Следует иметь в виду, что действие — сила, приложенная к телу Б, и противодействие — сила, приложенная к телу А, не уравновешиваются, так как они приложены к разным телам.
  • Закон 6 (закон отвердевания). Равновесие нетвердого тела не нарушается при его затвердевании. Не следует при этом забывать, что условия равновесия, являющиеся необходимыми и достаточными для твердого тела, являются необходимыми, но недостаточными для соответствующего нетвердого тела.
  • Закон 7 (закон освобождаемости от связей). Несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив действие связей соответствующими реакциями связей.
    Связи и их реакции
  • Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности.
  • Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры.
  • Шарнирная неподвижная опора противодействует любому перемещению в плоскости, перпендикулярной оси вращения.
  • Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня.
  • Глухая заделка противодействует любому перемещению и вращению в плоскости. Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.
    Момент силы относительно точки
  • Абсолютное значение момента равно произведению модуля силы на кратчайшее расстояние h от центра вращения до линии действия силы. Расстояние h называют плечом силы.
  • Момент считают положительным, если сила стремится вращать плечо h против хода часовой стрелки и отрицательным при вращении по ходу часовой стрелки.
  • Свойства момента силы относительно точки: 1) Момент силы не изменится при переносе точки приложения силы вдоль линии действия силы. 2) Момент силы равен нулю, если линия действия силы проходит через точку приложения силы. 3) Момент равнодействующей силы относительно точки равен сумме моментов слагаемых сил относительно этой точки.

    ,

    где
    Момент силы относительно оси
  • Момент силы относительно оси — это момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью. Момент считается положительным, если с положительного конца оси поворот, который сила стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.

  • Чтобы найти момент силы относительно оси, нужно: 1) Провести плоскость перпендикулярную оси z. 2) Спроецировать силу на эту плоскость и вычислить величину проекции . 3) Провести плечо h из точки пересечения оси с плоскостью на линию действия проекции силы и вычислить его длину. 4) Найти произведение этого плеча и проекции силы с соответствующим знаком.
  • Свойства момента силы относительно оси. Момент силы относительно оси равен нулю, если:

    1) , то есть сила параллельна оси.

    2) h=0, то есть линия действия силы пересекает ось.
    Момент пары сил
  • Момент пары сил равен произведению одной силы на кратчайшее расстояние между линиями действия сил пары, которое называется плечом пары (пара сил оказывает на тело вращающее действие) , где: — силы, составляющие пару; h — плечо пары. Момент пары считают положительным, если силы стремятся вращать плечо против хода часовой стрелки.
  • Свойства пары сил. 1) Сумма проекций сил пары на любую ось равна нулю. 2) Не изменяя момента пары можно одновременно соответственно изменять значение сил и плечо пары.

    3) Пару можно переносить в плоскости ее действия при этом действие пары на тело не изменится.

    Преобразование сходящейся системы сил
  • Равнодействующая двух сходящихся сил находится на основании аксиомы о параллелограмме сил. Геометрическая сумма любого числа сходящихся сил может быть определена путем последовательного сложения двух сил – способ векторного многоугольника.

    Вывод: система сходящихся сил () приводится к одной равнодействующей силе .

  • Аналитически равнодействующая сила может быть определена через ее проекции на оси координат: Согласно теореме: проекция равнодействующей на ось равна сумме проекций слагаемых сил на эту ось: , или в общем виде С учетом равнодействующая определяется выражением: .
  • Направление вектора равнодействующей определяется косинусами углов между вектором и осями x, y, z:
    Преобразование произвольной системы сил
  • Теорема: силу, приложенную к твердому телу, можно, не изменяя оказываемого ею действия, перенести параллельно в другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы относительно точки, в которую она переносится. В результате указанного преобразования получается сходящаяся система сил и сумма моментов пар сил. Действие сходящейся системы сил заменяют действием суммарной силы, действие моментов — суммарным моментом.

    Суммарный вектор — это главный вектор системы сил.

    Суммарный момент — это главный момент системы сил. Вывод: произвольная система сил в результате тождественного преобразования приводится к главному вектору и главному моменту системы сил.
  • Аналитически главный вектор и главный момент системы сил могут быть определены через их проекции на оси координат: ,
    Условия равновесия систем сил
  • Равновесие системы сходящихся сил Действие системы сходящихся сил эквивалентно действию одной равнодействующей силы.

    Для равновесия тела необходимо и достаточно, чтобы равнодействующая равнялась нулю .

    Из формулы следует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю:
  • Для равновесия плоской сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y равнялась нулю:
    Равновесие произвольной системы сил.
  • Действие произвольной системы сил эквивалентно действию главного вектора и главного момента. Для равновесия необходимо и достаточно выполнения условия: .
  • Для равновесия произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси X,Y,Z и суммы моментов всех сил относительно осей X,Y,Z равнялись нулю:
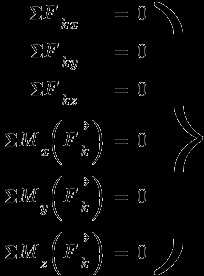
  • Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций главного вектора на оси X,Y, и алгебраическая сумма моментов сил относительно центра О были равны нулю:

Кинематика

Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.

    Основные понятия кинематики
  • Закон движения точки (тела) – это зависимость положения точки (тела) в пространстве от времени.
  • Траектория точки – это геометрическое место положений точки в пространстве при ее движении.
  • Скорость точки (тела) – это характеристика изменения во времени положения точки (тела) в пространстве.
  • Ускорение точки (тела) – это характеристика изменения во времени скорости точки (тела).
    Способы задания движения точки
  • Задать движение точки — значит задать изменение ее положения по отношению к выбранной системе отсчета. Существуют три основные системы отсчета: векторная, координатная, естественная.
  • В векторной системе положение точки относительно начала отсчета задается радиус-вектором. Закон движения: .
  • В системе координат OXYZ положение точки задается тремя координатами X, Y, Z. Закон движения: x = x(t), y = y(t); z = z(t).
  • В естественной системе отсчета положение точки задается расстоянием S от начала отсчета до этой точки вдоль траектории. Закон движения: . Движение точки, при естественном способе задания движения, определено если известны: 1) Траектория движения. 2) Начало и направление отсчета дуговой координаты. 3) Уравнение движения. При естественном способе задания движения, в отличии от других способов, используются подвижные координатные оси, движущиеся вместе с точкой по траектории. Такими осями являются:

    Касательная (τ) – направлена в сторону возрастания дуговой координаты по касательной к траектории.

    Главная нормаль (n) – направлена в сторону вогнутости кривой. Бинормаль (b) – направлена перпендикулярно к осям τ, n.
    Определение кинематических характеристик точки
  • Траектория точки В векторной системе отсчета траектория описывается выражением: . В координатной системе отсчета траектория определяется по закону движения точки и описывается выражениями z = f(x,y) — в пространстве, или y = f(x) – в плоскости. В естественной системе отсчета траектория задается заранее.
  • Определение скорости точки в векторной системе координат При задании движения точки в векторной системе координат отношение перемещения к интервалу времени называют средним значением скорости на этом интервале времени: . Принимая интервал времени бесконечно малой величиной, получают значение скорости в данный момент времени (мгновенное значение скорости): . Вектор средней скорости направлен вдоль вектора в сторону движения точки, вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки. Вывод: скорость точки – векторная величина, равная производной от закона движения по времени. Свойство производной: производная от какой либо величины по времени определяет скорость изменения этой величины.
  • Определение скорости точки в координатной системе отсчета Скорости изменения координат точки:

    .

    Модуль полной скорости точки при прямоугольной системе координат будет равен:

    .

    Направление вектора скорости определяется косинусами направляющих углов:

    ,

    где — углы между вектором скорости и осями координат.
  • Определение скорости точки в естественной системе отсчета Скорость точки в естественной системе отсчета определяется как производная от закона движения точки: . Согласно предыдущим выводам вектор скорости направлен по касательной к траектории в сторону движения точки и в осях определяется только одной проекцией .
    Ускорение точки
  • По определению ускорение характеризует изменение скорости, то есть скорость изменения скорости.
  • Ускорения точки в векторной системе отсчета На основании свойства производной:

    .

    Вектор скорости может изменяться по модулю и направлению.

    Вектор ускорения направлен по линии приращения вектора скорости, т. е. в сторону искривления траектории.

  • Ускорение точки в координатной системе отсчета Ускорение изменения координат точки равно производной по времени от скоростей изменения этих координат:

    .

    Полное ускорение в прямоугольной системе координат будет определяться выражением:

    .

    Направляющие косинусы вектора ускорения:

    .

  • Ускорение точки в естественной системе отсчета Приращение вектора скорости можно разложить на составляющие, параллельные осям естественной системы координат: . Разделив левую и правую части равенства на dt, получим: , где — тангенциальное ускорение; — нормальное ускорение; R — радиус кривизны траектории в окрестности точки.
    Кинематика твердого тела
  • В кинематике твердых тел решаются две основные задачи: 1) задание движения и определение кинематических характеристик тела в целом;

    2) определение кинематических характеристик точек тела.

  • Поступательное движение твердого тела Поступательное движение — это движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению.

    Теорема: при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения.

    Вывод: поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки.
  • Вращательное движение твердого тела вокруг неподвижной оси Вращательное движение твердого тела вокруг неподвижной оси — это движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.

    Положение тела определяется углом поворота . Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)

    Закон вращательного движения тела вокруг неподвижной оси . Угловую скорость и угловое ускорение тела определим методом дифференцирования:

    — угловая скорость, рад/с;

    — угловое ускорение, рад/с². Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точку М, то точка М будет описывать вокруг точки С окружность радиуса R. За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние . Модуль линейной скорости:

    .

    Ускорение точки М при известной траектории определяется по его составляющим : , где . В итоге, получаем формулы

    тангенциальное ускорение: ;

    нормальное ускорение: .
    Плоско-параллельное движение твердого тела
  • Плоско-параллельное движение твердого тела — это движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных одной неподвижной плоскости. Движение сечения S в своей плоскости можно рассматривать как сложное, состоящее из двух элементарных движений: 1) поступательного и вращательного;

    2) вращательного относительно подвижного (мгновенного) центра.

  • В первом варианте движение сечения может быть задано уравнениями движения одной его точки (полюса) и вращением сечения вокруг полюса. В качестве полюса может быть принята любая точка сечения. Уравнения движения запишутся в виде:

    .

    Ускорение точки движущейся плоской фигуры складывается из ускорения полюса относительно неподвижной системы отсчета и ускорения за счет вращательного движения вокруг полюса.

  • Во втором варианте движение сечения рассматривается как вращательное вокруг подвижного (мгновенного) центра P. В этом случае скорость любой точки В сечения будет определяться по формуле для вращательного движения: . Угловая скорость вокруг мгновенного центра Р может быть определена если известна скорость какой либо точки сечения, например точки А. .
  • Положение мгновенного центра вращения может быть определено на основании следующих свойств: 1) вектор скорости точки перпендикулярен радиусу;

    2) модуль скорости точки пропорционален расстоянию от точки до центра вращения ();

    3) скорость в центре вращения равна нулю.
  • Теорема: проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки, равны между собой и одинаково направлены. Доказательство: расстояние АВ изменяться не может, следовательно, не может быть больше или меньше . Вывод: .
    Сложное движение точки
  • Относительное движение — это движение точки относительно подвижной системы. Переносное движение — это движение точки вместе с подвижной системой. Абсолютное движение — это движение точки относительно неподвижной системы. Соответственно называют скорости и ускорения:

    — относительные;

    — переносные; — абсолютные.
  • Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей (согласно теореме о сложении скоростей): . Абсолютное значение скорости определяется по теореме косинусов:

    .

  • Ускорение по правилу параллелограмма определяется только при поступательном переносном движении . .
  • При непоступательном переносном движении появляется третья составляющая ускорения, называемое поворотным или кориолисовым. , где . Кориолисово ускорение численно равно:

    ,

    где – угол между векторами и . Направление вектора кориолисова ускорения удобно определять по правилу Н.Е. Жуковского: вектор спроектировать на плоскость, перпендикулярную оси переносного вращения, проекцию повернуть на 90 градусов в сторону переносного вращения. Полученное направление будет соответствовать направлению кориолисова ускорения.

Динамика

Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.

    Основные понятия динамики
  • Инерционность — это свойство материальных тел сохранять состояние покоя или равномерного прямолинейного движения, пока внешние силы не изменят этого состояния.
  • Масса — это количественная мера инерционности тела. Единица измерения массы — килограмм (кг).
  • Материальная точка — это тело, обладающее массой, размерами которого при решении данной задачи пренебрегают.
  • Центр масс механической системы — геометрическая точка, координаты которой определяются формулами: где mk, xk, yk, zk — масса и координаты k-той точки механической системы, m — масса системы. В однородном поле тяжести положение центра масс совпадает с положением центра тяжести.
  • Момент инерции материального тела относительно оси – это количественная мера инертности при вращательном движении. Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси:

    .

    Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек:

  • Сила инерции материальной точки — это векторная величина, равная по модулю произведению массы точки на модуль ускорения и направленная противоположно вектору ускорения:
  • Сила инерции материального тела — это векторная величина, равная по модулю произведению массы тела на модуль ускорения центра масс тела и направленная противоположно вектору ускорения центра масс: , где — ускорение центра масс тела.
  • Элементарный импульс силы — это векторная величина , равная произведению вектора силы на бесконечно малый промежуток времени dt: . Полный импульс силы за Δt равен интегралу от элементарных импульсов:

    .

  • Элементарная работа силы — это скалярная величина dA, равная скалярному произведению вектора силы на бесконечно малое перемещение . Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов:

    ,

    где α — угол между направлениями векторов перемещения и силы.
  • Работа силы на конечном перемещении точки её приложения равна интегралу от элементарной работы, взятому по перемещению: . Единица измерения работы — Джоуль (1 Дж = 1 Н·м).
  • Количество движения материальной точки — это векторная величина , равная произведению массы m на её скорость : .
  • Количество движения механической системы равно векторной сумме количества движения её точек. или , где m — масса механической системы, — вектор скорости центра масс системы.
  • Кинетическая энергия материальной точки — это скалярная величина Т, равная половине произведения массы точки на квадрат её скорости: .
  • Кинетическая энергия механической системы равна сумме кинетических энергий всех её точек: .
    Аксиомы динамики
  • Первая аксиома — это закон инерции. Если на свободную материальную точку не действуют никакие силы или действует уравновешенная система сил, то точка будет находиться в состоянии покоя или равномерного прямолинейного движения.
  • Вторая аксиома — закон пропорциональности ускорения. Ускорение, сообщаемое материальной точке действующей на неё силой, пропорционально этой силе и по направлению совпадает с направлением силы: — это основной закон динамики.
  • Третья аксиома — это закон противодействия. Силы, с которыми действуют друг на друга две материальные точки, равны по модулю и направлены вдоль прямой, соединяющей эти точки, в противоположные стороны:

    .

  • Четвертая аксиома — закон независимости действия сил. При действии на материальную точку системы сил полное ускорение этой точки равно геометрической сумме ускорений от действия каждой силы:

    Дифференциальные уравнения динамики
  • Дифференциальные уравнения движения точки связывают ускорение точки с действующими на нее силами. Фактически дифференциальные уравнения являются записью основного закона динамики в явной дифференциальной форме. Для абсолютного движения точки (движение в инерциальной системе отсчета) дифференциальное уравнение имеет вид:

    .

  • Векторное уравнение может быть записано в проекциях на оси прямоугольной инерциальной системы координат:
  • При известной траектория движения точки уравнение может быть записано в проекциях на оси естественной системы координат: С учетом того, что , где — тангенциальное ускорение; — нормальное ускорение, уравнения примут вид:

    Общие теоремы динамики
  • Общие теоремы динамики устанавливают зависимость между мерами механического движения и механического взаимодействия. Выводы теорем являются результатом тождественного преобразования основного закона динамики.
  • Теорема об изменении количества движения: изменение количества движения материальной точки (механической системы) за конечный промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени — для материальной точки; — для механической системы.
  • Теорема об изменении кинетической энергии: изменение кинетической энергии точки (механической системы) при её перемещении равно сумме работ всех действующих внешних сил на этом перемещении — для материальной точки; — для механической системы.
  • Кинетическая энергия механической системы определяется в соответствии с , при этом для твердых тел выведены следующие зависимости: — при поступательном движении тела; — при вращательном движении тела; — при плоско-параллельном движении тела.
  • Момент инерции цилиндра относительно его оси: .
  • Момент инерции стержня относительно оси z: .
  • Момент инерции прямоугольной пластины относительно осей х и y: .
  • Момент инерции шара определяется по формуле: .
  • Работа силы тяжести: , где P — сила тяжести; h — изменение положения тела по вертикали.
  • Работа силы при вращательном движении тела , где M — момент силы, w — угловая скорость тела. Следует иметь в виду, что работа, как скалярная величина, может быть положительной или отрицательной. Работа будет положительной если направление действия силы совпадает с направлением движения.
    Принцип Даламбера
  • Формулировка принципа Даламбера: если в любой момент времени к действующим на точку силам присоединить силы инерции, то полученная система сил будет уравновешенной: .
  • Для механической системы: .

Примеры решения задач

Решение примеров по теме: «Статика твердого тела»

Пример 1. Условия равновесия

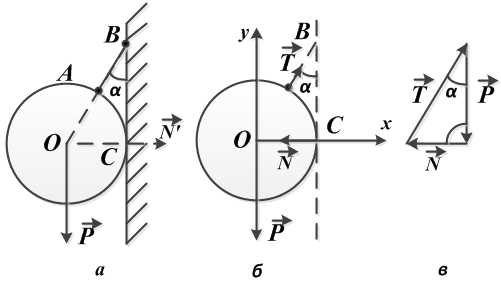Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.

Дано: P = 10 Н; α = 45° Найти: N, T — ?

Решение. Отбрасываем связи, а их действие на шар заменяем реакциями.

Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.

Тем самым выявляется полная система сил, приложенных к покоящемуся шару.

Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).

Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).

При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).

В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:

После подстановки в формулы числовых значений, получим: .

Дано: Движение точки задано уравнениями ; (x, у — в сантиметрах, t — в секундах). Найти: уравнение траектории точки в координатной форме.

Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла: .

Опуская промежуточные выражения, получаем уравнение траектории: .

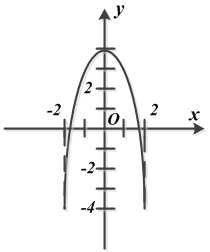Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).

Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.

Дано: m = 10 кг; a = 0,5 м/с2. Найти: F — ?

Решение. Согласно основному закону динамики: .

Подставив значения в формулу, получим:

Ответ: сила, сообщающая массе, равной 10 кг, ускорение 0,5 м/с2, равна 5 Н.

Список литературы: Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах.

Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие.

Смотрите также

 

"Питер - АТ"
ИНН 780703320484
ОГРНИП 313784720500453

Новости